# 数据结构的分类
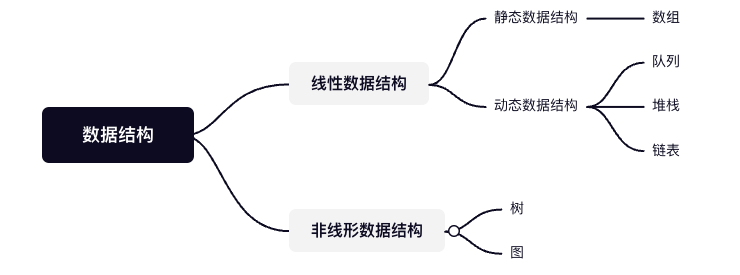
- 线形数据结构:数据元素按顺序或线形排列的数据结构,其中每一个元素都附加到其上一个和下一个相邻元素。
- 静态数据结构:具有固定的内存大小,访问更加容易。
- 动态数据结构:大小不固定,可以在运行期间随机更新,更加灵活节省空间。
- 非线性数据结构:数据元素不按顺序或线形放置,只能在一次运行中遍历所有元素。
# 线性数据结构简介
元素在一维钟排列,也称为线性维度
# 特点
- 顺序组织:每个元素都有一个唯一前驱和唯一后继(首位除外)。
- 顺序保留:保留元素被添加到数据结构的顺序。
- 固定或动态大小:可以固定或动态大小。
- 高效访问:访问线性数据结构十分高效
# 常见线性数据结构
- 数组:存储在连续内存位置的元素的集合。
- 链表:节点的集合,每个节点包含一个元素和对下一个节点的引用。(数据+指针)
- 堆栈:后进先出LIFO的元素集合
- 队列:先进后出FIFO的元素集合
# 数组
# 特点
- 同质元素:数组中的元素必须相同类型
- 连续内存分配:数组中的元素在连续的内存位置
- 从零开始的索引
- 随机访问:数组提供对元素的恒定时间访问(时间复杂度O(1))。无论数组大小如何,访问任何元素需要的时间是一样的。
# 操作
- 访问元素:O(1)。
- 插入:末尾O(1),其他O(n)。
- 删除:末尾O(1),其他O(n)。
- 搜索:线性搜索O(n),二分O(logn)。
# 链表
# 特点
- 节点:每个元素都是一个节点,包含数据和指针。
- 头:链表中的第一个节点。
- 尾部:链表中的最后一个节点
# 链表类型
- 单链表:常规单向链表。如1->2->NULL
- 双向链表:每个节点有两个指针,一个指向后一个,一个指向前一个,允许两个方向的遍历。
- 循环链表:第一个和最后一个节点连接,末尾没有NULL。
# 操作
- 访问元素:O(n)。
- 搜索:O(n)。
- 插入:有插入位置时,O(1)。
- 删除:有删除的位置时,O(1)。
# 堆栈
# 类型
固定大小:会发生堆栈溢出错误,为空删除时也会出现下溢错误。 动态大小:堆栈满的时候会自动增加容量,为空时会减少大小,用链表实现,允许挑战栈的大小。
# 操作
push:推入一个元素。 pop:推出一个元素。 top:返回最后插入的元素。 size:返回堆栈的大小,即存在的元素总数。 isEmpty:堆栈是否为空。
# 队列
# 类型
- 输入受限队列:只能从一端获取输入,可以从任意一段删除。
- 输出受限队列:两端都可以获取输入,只能从一端删除。
- 循环队列:最后一个位置连接回第一个位置。
- 双端队列:两端都可以插入删除。
- 优先级队列:根据分配给元素的优先级访问。
# 操作
- Enqueue():将一个元素添加到队尾。
- Dequeue():从队列中移除元素。
- Peek()或front():获取队列前端节点可用的数据元素,但不删除。
- after():获取队列后端元素,但不删除。
- isFull():是否已满。
- isNull():是否为空。
# 非线性数据结构
元素以一对多,多对一和多对多维度排列。
# 二叉树
树是分层数据结构。二叉树是一种树形结构,每个节点最多有两个子节点,分别为左子节点和右子节点。主要用链表来实现。二叉树由指向树中最顶层节点的指针表示。如果树为空,则 root 的值为 NULL。 二叉树包含三部分:数据、左节点指针、右节点指针。
# 二叉搜索树
# 是具有以下附属属性的二叉树:
- 根节点的左侧部分的key比根节点小
- 根节点的右侧部分的key比根节点大
- 不存在重复的key
# 堆
堆是一种基于树的特殊数据结构,其中树是完全二叉树。一般有两种类型:
- 最大堆:根节点的key必须比左右子节点都大,此规则递归到最后一层。
- 最小堆:根节点的key必须比左右子节点都小,此规则递归到最后一层。